- IoU
Intersection over Union, is used to evaluate the performance of object detection by comparing the ground truth bounding box to the preddicted bounding box.
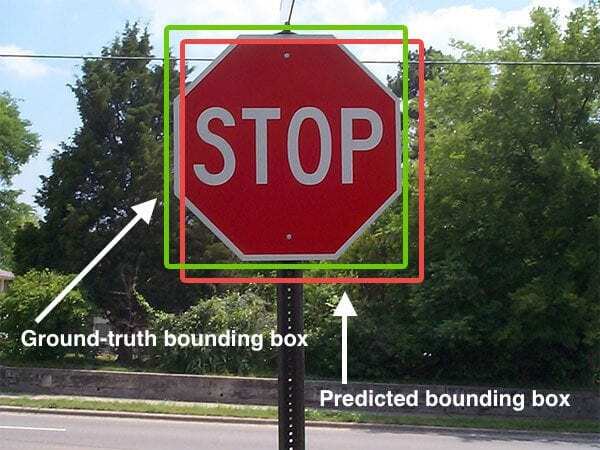
- Ground Truth bounding box
Hand labeled, the actual images themselves.
- Computing Intersection over Union
It can therefore be determined via :
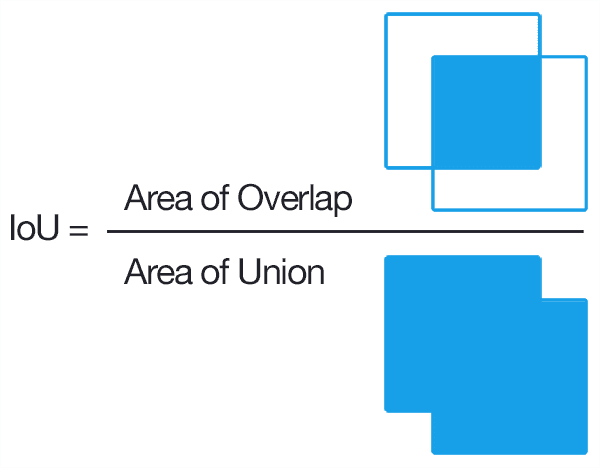
- The numerator : we compute the area of overlap between the predicted bounding box and the ground-truth bounding box.
- The denominator : is the area of union, or more simply, the area encompassed by both the predicted bounding box and the ground-truth bounding box.
For example :
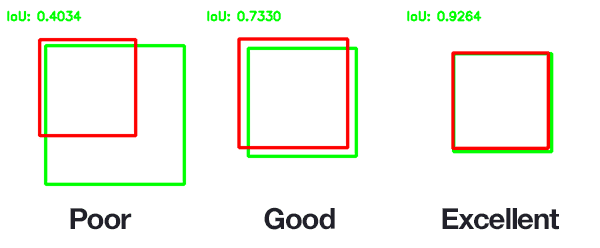
The predicted bounding boxes that heavily overlap with the ground-truth bounding boxes have higher scores than those with less overlap. This makes Intersection over Union an excellent metric for evaluating custom object detectors.
- calculate IoU

and stand for the bounding box's top-left corner coordinates, while and stand for the bounding box's bottom-right corner coordinates.
There is one condition that needs to be met:
When the boxes don’t intersect, IoU cannot be calculated.
The overlap and the union parts of boxes X and Y are calculated. Equation (10) help us calculate the intersection points using the overlap boundary points, whereas equations (11) and (12) are used for calculating n(X) and n(Y) of the set X and Y.
Equations 13, on the other hand, is the union formula which is the sum of individual n(X) and n(Y) minus the intersection of both. Using Eq. (12) and Eq. (10), we can calculate Eq. (14).
Let's say that the ground truth bounding box for a picture of a dog is [A1=50, B1=100, C1=200, D1=300]
and the predicted bounding box is [A2=80, B2=120, C2=220, D2=310].
The visual representation of the box is shown below:
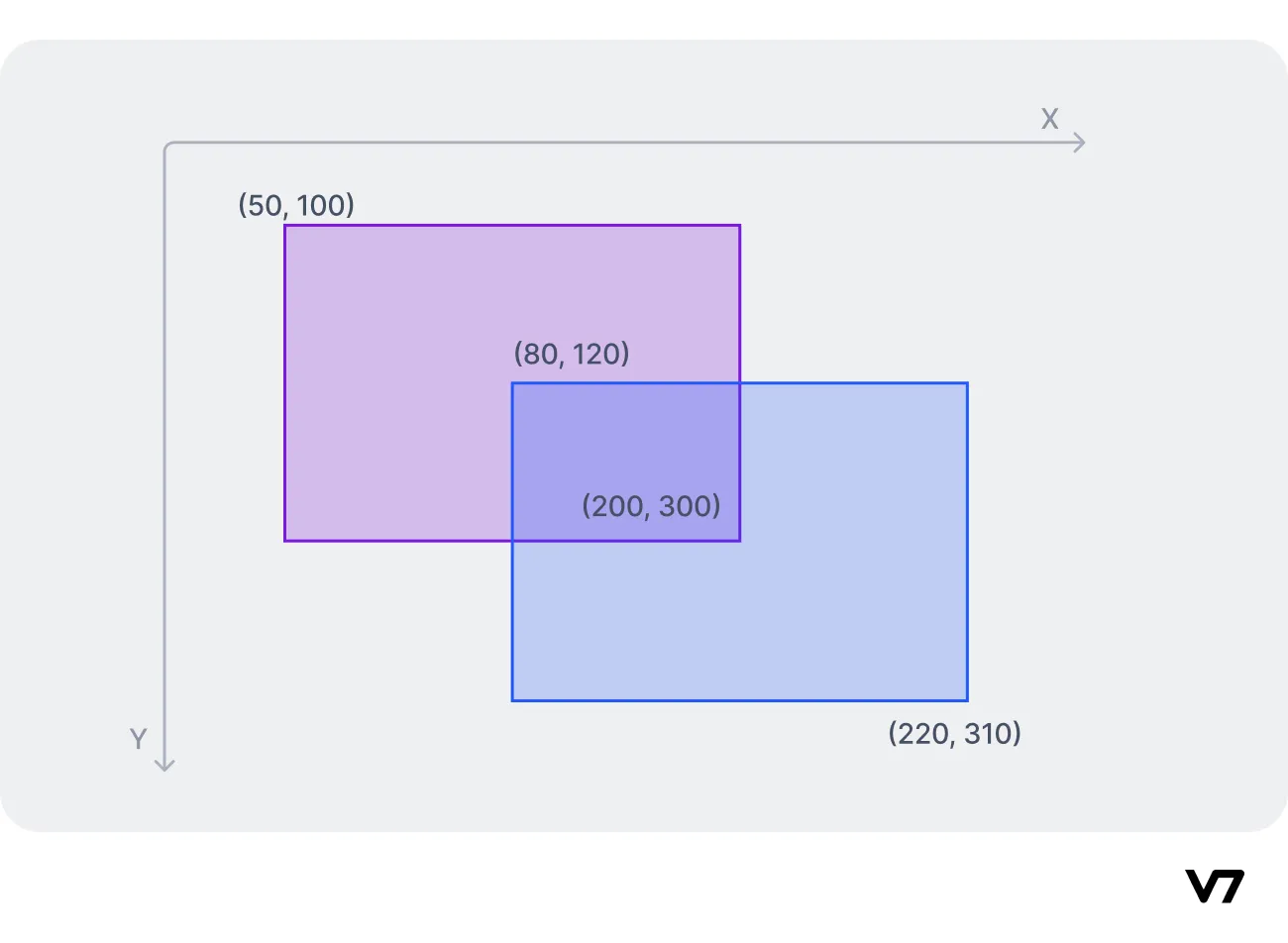
The calculation is as follows:
To calculate the IoU score, we can now enter the following values into the IoU formula:
def calculate_iou(gt_bbox, pre_bbox):
"""
args
gt_bbox[array]:1*4 single gt bbox
pre_bbox[array]:1*4 single pre bbox
return
iou[float]:iou between 2bboxes
"""
xmin=np.max([gt_bbox[0],pre_bbox[0]])
ymin=np.max([gt_bbox[1],pre_bbox[1]])
xmax=np.min([gt_bbox[2],pre_bbox[2]])
ymax=np.min([gt_bbox[3],pre_bbox[3]])
intersection = max(0, xmax - xmin) * max(0, ymax - ymin)
gt_area=(gt_bbox[2]-gt_bbox[0])*(gt_bbox[3]-gt_bbox[1])
pred_area=(pre_bbox[2]-pre_bbox[0])*(pre_bbox[3]-pre_bbox[1])
union=gt_area+pred_area-intersection
return intersection/union, [xmin, ymin, xmax, ymax]
'Deep Learning > Object Detection' 카테고리의 다른 글
| R-CNN (0) | 2024.01.23 |
|---|---|
| (prerequisite-R-CNN) Non-maximum Suppression(NMS) (0) | 2024.01.23 |
| (prerequisite-R-CNN) Bounding Box Regression (0) | 2024.01.23 |
| (prerequisite-R-CNN) RoI(Region of Interest), Quantization, RoI Align (0) | 2024.01.20 |
| (prerequisite-R-CNN) Selective Search (0) | 2024.01.19 |