- Time of Flight(ToF)

- The measurement of the time taken by an object, particle, or wave to travel a distance.
- ToF sensors use a tiny laser to fire out infrared light where the light produced will bounce off any object and return to the sensor. Based on the time difference between the emission of the light and its return to the sensor after being reflected by an object, the sensor is able to measure the distance between the object and the sensor.
- merits and demerits of Time of Flight(ToF)
Merits
- Excellent distance decomposition capability
- Accurate and fast
- Relatively inexpensive
- Precise measurements of long distances and ranges
- Real-time is possible
Demerits
- The sensing distance is limited because the light weakens when it hits the object and returns.
- The distance measurement is impossible under sunlight.
- Relatively large
- Using Timed Pulses
It works by firstly illuminating the target with laser light and measuring the reflected light with a scanner where the distance of the object is deduced using the speed of light to calculate the distance traveled accurately. In addition, the differences in laser return times and wavelengths are then used to make precise digital 3D representations and surface characteristics of the target and visually map out its individual features.

As you can see above, that is the process where the laser light is first emitted and bounced off an object back to the sensor. With the laser return time, ToF cameras are able to measure the exact distance in a short time given the speed at which light travels(ToF is translated into the distance).
- The formula to get the precise distance
(Speed of light x Time of flight) / 2
- ToF Time Pulses

A timer will start during the exit of the light and when the return light is received by the receiver, the time is returned by the timer. When the two times are subtracted, the “time of flight” of the light is obtained, and the speed of light is constant, so the distance can be easily calculated using the formula above. With this, all points on the object’s surface can be determined.
- Using Phase Shift of an Amplitude Modulated Wave
ToF can also use continuous waves to detect the phase shift of the reflected light to determine depth and distance.

By modulating the amplitude, it creates a light source of a sinusoidal form with a known frequency which allows a detector to be able to determine the phase shift of the reflected light.
- Period
It goes from one peak to the next (or from any point to the next matching point).

- Amplitude
It is the height from the center line to the peak (or to the trough). Or we can measure the height from highest to lowest points and divide that by 2.
- Phase Shift

It is how far the function is shifted horizontally from the usual position.
- Vertical Shift

It is how far the function is shifted vertically from the usual position.
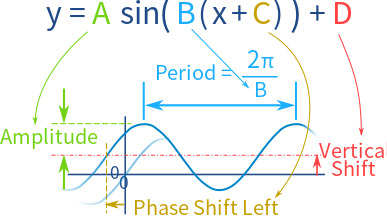
- The formula which has all of them in one equation
A : amplitude
2π/B : period
C : phase shift (positive is to the left)
D : vertical shift
1. Example: sin(x)
| amplitude A = 1 period 2π/B = 2π/4 = 2π 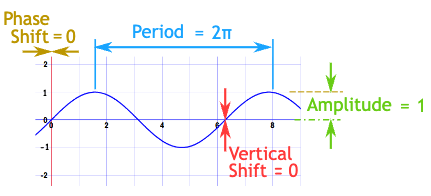 |
2. Example : 2 sin(4(x − 0.5)) + 3
| amplitude A = 2 period 2π/B = 2π/4 = π/2 phase shift = −0.5 (or 0.5 to the right) vertical shift D = 3 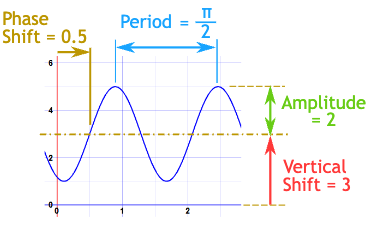 - the 2 tells us it will be 2 times taller than usual, so Amplitude = 2 - the usual period is 2π, but in our case that is "sped up" (made shorter) by the 4 in 4x, so Period = π/2 - the −0.5 means it will be shifted to the right by 0.5 - astly the +3 tells us the center line is y = +3, so Vertical Shift = 3 |
3. Example :
Instead of x we can have t (for time) or maybe other variables.
First we need brackets around the (t+1), so we can start by dividing the 1 by 100:
3 sin(100t + 1) = 3 sin(100(t + 0.01))
| amplitude is A = 3 period is 2π/100 = 0.02 π phase shift is C = 0.01 (to the left) vertical shift is D = 0 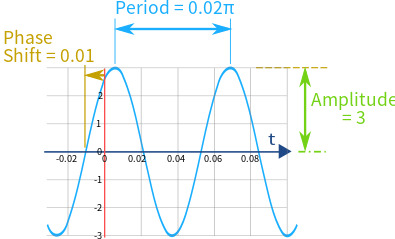 |
- Frequency
It is how often something happens per unit of time (per "1").
When frequency is per second it is called "Hertz".
For example, 50 Hertz means 50 times per second.
- The relation between the Period and Frequency
1. Example: Here the cosine function repeats 4 times between 0 and 1:
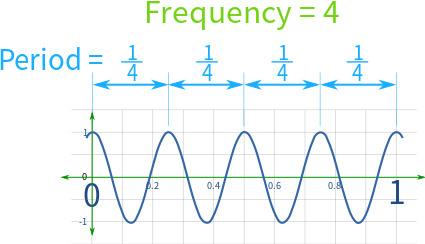 So the Frequency is 4 And the Period is 1/4 |
2. Example: 3 sin(100(t + 0.01))
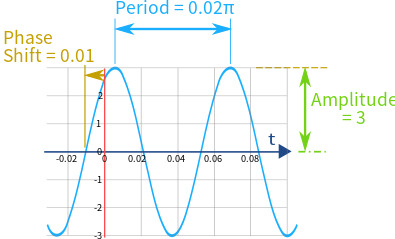 The period is 0.02π So the Frequency is 1/0.02π = 50/π |
https://www.mathsisfun.com/algebra/amplitude-period-frequency-phase-shift.html
'Autonomous Vehicle > Sensors' 카테고리의 다른 글
| Sensor Selection Criteria (0) | 2023.10.05 |
|---|---|
| Radar VS Lidar 2 (0) | 2023.10.04 |
| IMU, MEMS, Foucault pendulum, Coriolis force (0) | 2023.09.13 |
| GNSS, Degree of Freedom (0) | 2023.09.12 |
| Ultrasonic sensor, Trilateration (0) | 2023.08.29 |