- SVD(Singular Value Decomposition)
It is decomposed the matrix into three matrices when A is an m × n matrix.
Each of the three matrices meets the following conditions.
- Transposed Matrix
A matrix that changes rows and columns from the original matrix.
The symbol is appended to the right of an existing matrix representation. For example, if an existing matrix is , the transpose matrix is represented by .
- Identity Matrix(Unit Matrix or Elementary matrix)
It is the matrix which is n × n square matrix where the diagonal consist of ones and the other elements are all zeros.
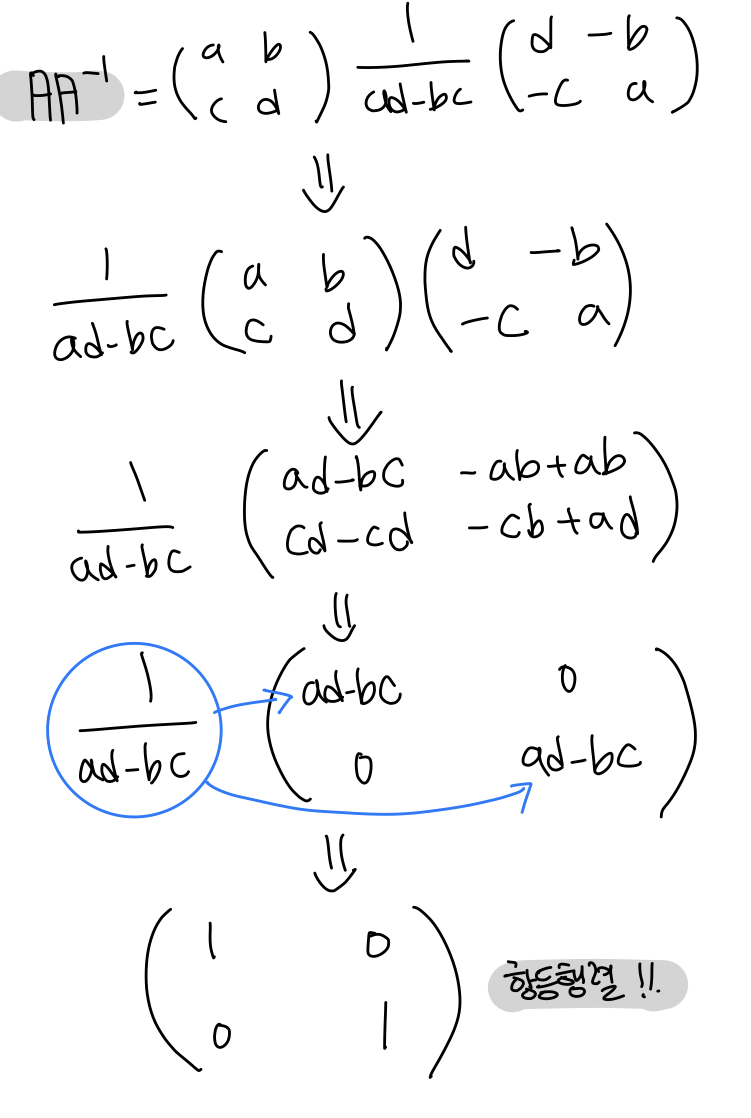
- Inverse Matrix
If matrix is multiplied by '?' matrix, and the result is an Identity Matrix, then the '?' matrix is called the Inverse Matrix of , and we call it .
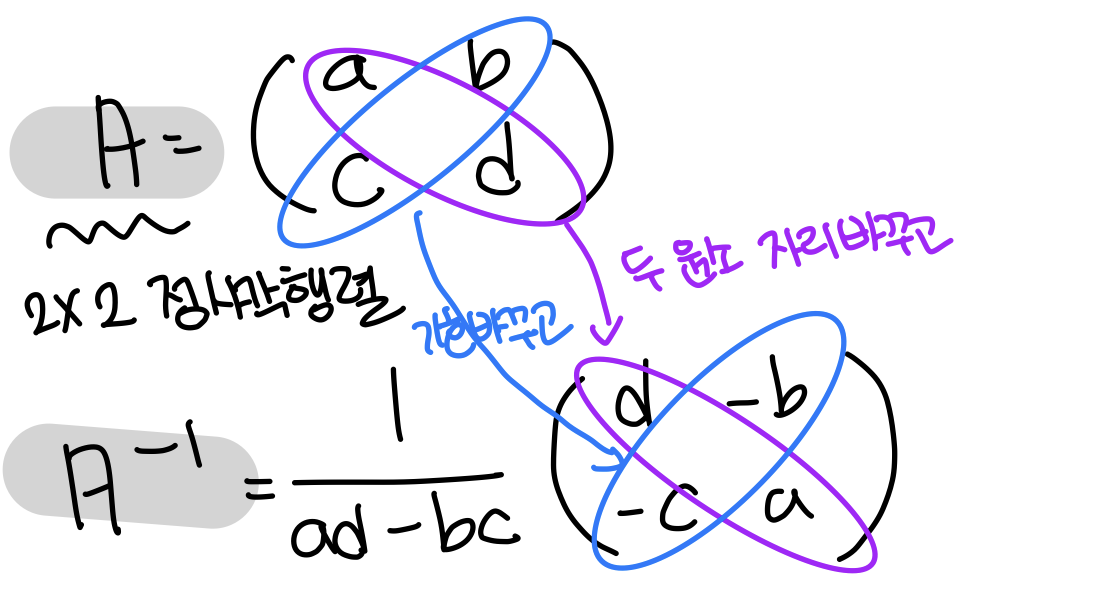
에 대해 이면 역행렬 는 다음과 같이 계산된다.
- Orthogonal matrix
we have a matrix A,
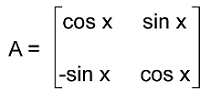
and its transpose matrix ,
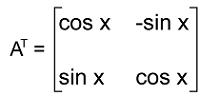
Now we will do the multiplication of both matrices in the following way,
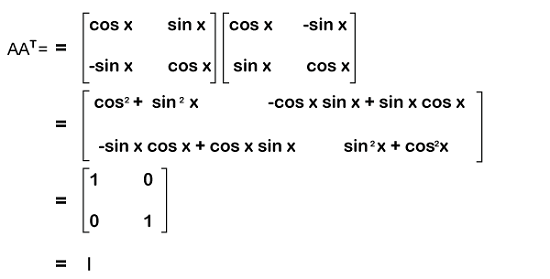
실수 행렬 에 대해서 를 만족하면서 을 만족하는 행렬 를 직교 행렬이라고 합니다. 그런데 역행렬의 정의를 다시 생각해보면, 결국 직교 행렬은 를 만족합니다.
- Diagonal Matrix
A matrix in which the entries outside the main diagonal are all zero; the term usually refers to square matrices. Elements of the main diagonal can either be zero or nonzero.
- Rectangular Diagonal Matrix
The term diagonal matrix may sometimes refer to a rectangular diagonal matrix, which is a m-by-n matrix.
- When m × n matrix, m > n
- When m × n matrix, n > m
- Singular Value
A diagonal element of a diagonal matrix Σ.
When it expressed as σ1, σ2, σ3・・・, the Singular Value σ1, σ2, σ3・・・are sorted in descending order.
- Full SVD
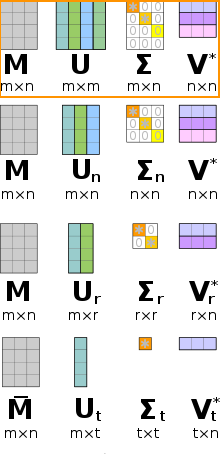

- Reduced SVDs
The decomposition of matrix m×n matrix A into SVD (where m>n).
- Thin SVD

Remove columns of U not corresponding to rows of V*.

- Compact SVD
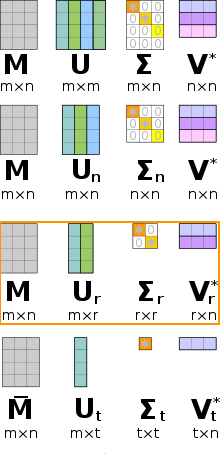
Remove vanishing singular values and corresponding columns/rows in U and V*.

Not only elements but also zero singular values are removed.
However, the calculated A becomes the same matrix as the original A.
- Truncated SVD
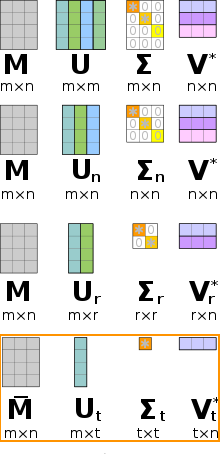
Keep only largest t singular values and corresponding columns/rows in U and V*.
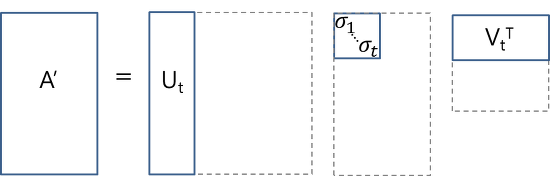
Non-zero singular value is also removed, in which case the original A is not preserved, and an approximate matrix A' comes out. The matrix A′ may be used for data compression, noise removal.
https://en.wikipedia.org/wiki/Singular_value_decomposition
https://darkpgmr.tistory.com/106
'Deep Learning > Object Detection' 카테고리의 다른 글
| Faster RCNN (0) | 2024.01.30 |
|---|---|
| Fast RCNN (0) | 2024.01.29 |
| SPPNet (0) | 2024.01.24 |
| (prerequisite-SPPNet) BOVW(Bag Of Visual Words) (0) | 2024.01.24 |
| R-CNN (0) | 2024.01.23 |