
- Bag of words(BoW)
It is a way of extracting features from text, a representation of text that describes the occurrence of words within a document, for example, pour the sentence into the bag and shuffling the bag, any information about the order or structure of words in the bag is discarded.
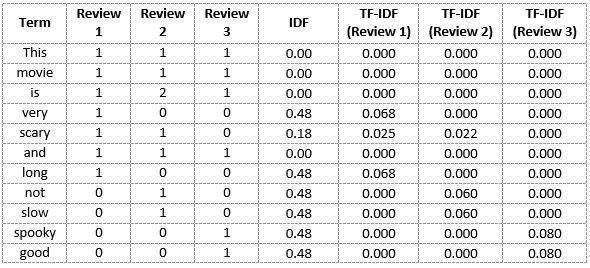
Review 1 : This movie is very scary and long
Review 2 : This movie is not scary and is slow
Review 3 : This movie is spooky and good

Reference : www.analyticsvidhya.com/blog/2020/02/quick-introduction-bag-of-words-bow-tf-idf/
- DTM or TDM
Document-Term Matrix or Term-Document Matrix, is a mathematical matrix that describes the frequency of terms that occur in a collection of documents. This is a matrix where
- each row represents one document
- each column represents one term (word)
- each value (typically) contains the number of appearances of that term in that document
It is often stored as a sparse matrix or sparse vector that most of value is 0.

- TF-IDF
Term Frequency-Inberse Document Frequency, is a technique to quantify a word in documents, we generally compute a weight to each word which signifies the importance of the word in the document and corpus.
1. TF
Term Frequency, measures the frequency of a word in a document.

The numerator N is the number of times the term 't' appears in the document 'd'.
Let's take the same vocabulary I had built above.
TF(‘movie’) = 1/8
TF(‘is’) = 2/8 = 1/4
TF(‘very’) = 0/8 = 0
TF(‘scary’) = 1/8
TF(‘and’) = 1/8
TF(‘long’) = 0/8 = 0
TF(‘not’) = 1/8
TF(‘slow’) = 1/8
TF( ‘spooky’) = 0/8 = 0
TF(‘good’) = 0/8 = 0
And now, let's calculate the term frequencies for all the terms and all the reviews.

2. IDF
Inverse Document Frequency, is how common or rare a word is in the entire document set. In other words, a measure of how important a term is. The closer it is to 0, the more common a word is. This metric can be calculated by taking the total number of documents, dividing it by the number of docments that contain a word. So, if the word is common and appears in many documents, this number will approach 0(log 1 is 0, in other words, numerator is same as denominator). Otherwise, it will approach 1.

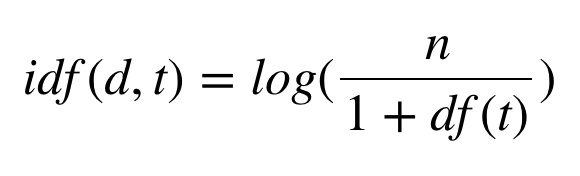
d : Document
t : Term(word)
n : Total Number of documents
IDF(‘movie’, ) = log(3/1+3)
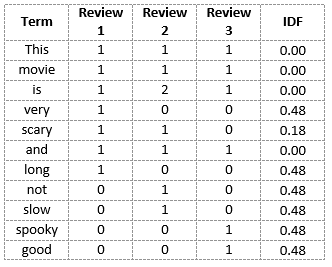
Hence, the words like “is”, “this”, “and”, etc., are reduced to 0 and have little importance, while words like “scary”, “long”, “good”, etc. are words with more importance and thus have a higher value.
Let's now calculate the TF-IDF score.
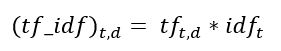
import pandas as pd
from math import log
docs=['This movie is very scary and long',
'This movie is not scary and is slow',
'This movie is spooky and good']
vocab=list(set(w for doc in docs for w in doc.split()))
vocab
>>>['is',
'slow',
'and',
'This',
'not',
'spooky',
'good',
'very',
'scary',
'movie',
'long']
vocab.sort()
N=len(docs)
def tf(t,d):
return d.count(t)
def idf(t):
df=0
for doc in docs:
df+=t in doc
return log(N/(1+df))
def tfidf(t,d):
return tf(t,d)*idf(t)
result=[]
for i in range(N):
result.append([])
d=docs[i]
for j in range(len(vocab)):
t=vocab[j]
result[-1].append(tf(t,d))
print(pd.DataFrame(result, columns=vocab))
print(result)
>>> This and good is long movie not scary slow spooky very
0 1 1 0 2 1 1 0 1 0 0 1
1 1 1 0 3 0 1 1 1 1 0 0
2 1 1 1 2 0 1 0 0 0 1 0
[[1, 1, 0, 2, 1, 1, 0, 1, 0, 0, 1], [1, 1, 0, 3, 0, 1, 1, 1, 1, 0, 0], [1, 1, 1, 2, 0, 1, 0, 0, 0, 1, 0]]
result=[]
for j in range(len(vocab)):
t=vocab[j]
result.append(idf(t))
pd.DataFrame(result, index=vocab, columns=['IDF'])
>>>
IDF
This -0.287682
and -0.287682
good 0.405465
is -0.287682
long 0.405465
movie -0.287682
not 0.405465
scary 0.000000
slow 0.405465
spooky 0.405465
very 0.405465
result=[]
for i in range(N):
result.append([])
d=docs[i]
for j in range(len(vocab)):
t=vocab[j]
result[-1].append(tfidf)
pd.DataFrame(result, columns=vocab)
- Python sklearn package
from sklearn.feature_extraction.text import TfidfVectorizer
corpus=['you know I want your love',
'I like you',
'what should I do ',]
tfidf=TfidfVectorizer().fit(corpus)
print(tfidf.transform(corpus).toarray())
print(tfidf.vocabulary_)
>>>[[0. 0.46735098 0. 0.46735098 0. 0.46735098
0. 0.35543247 0.46735098]
[0. 0. 0.79596054 0. 0. 0.
0. 0.60534851 0. ]
[0.57735027 0. 0. 0. 0.57735027 0.
0.57735027 0. 0. ]]
{'you': 7, 'know': 1, 'want': 5, 'your': 8, 'love': 3, 'like': 2, 'what': 6, 'should': 4, 'do': 0}