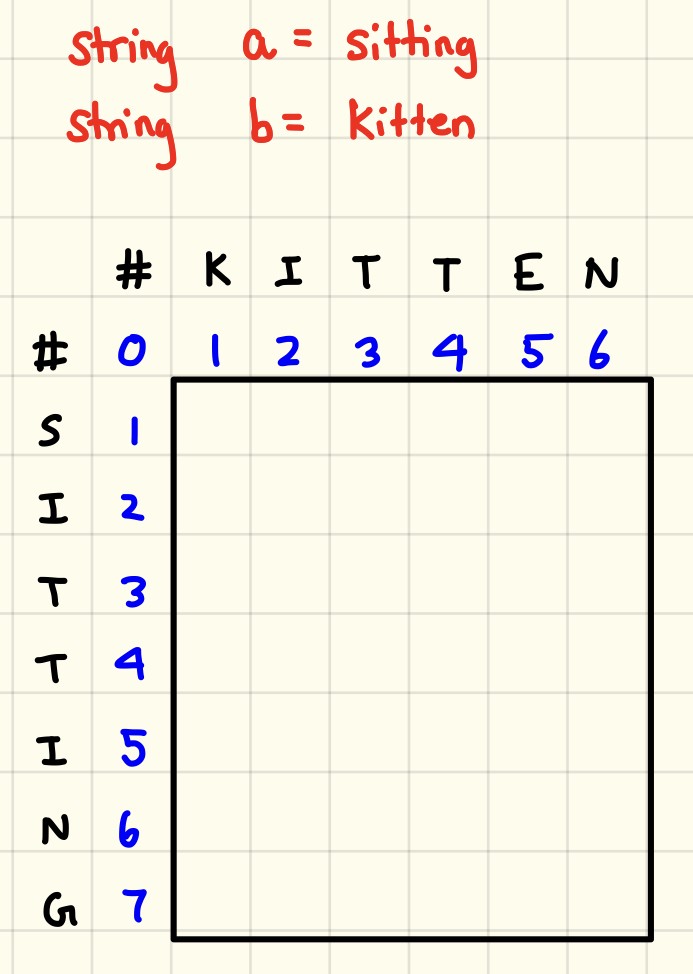
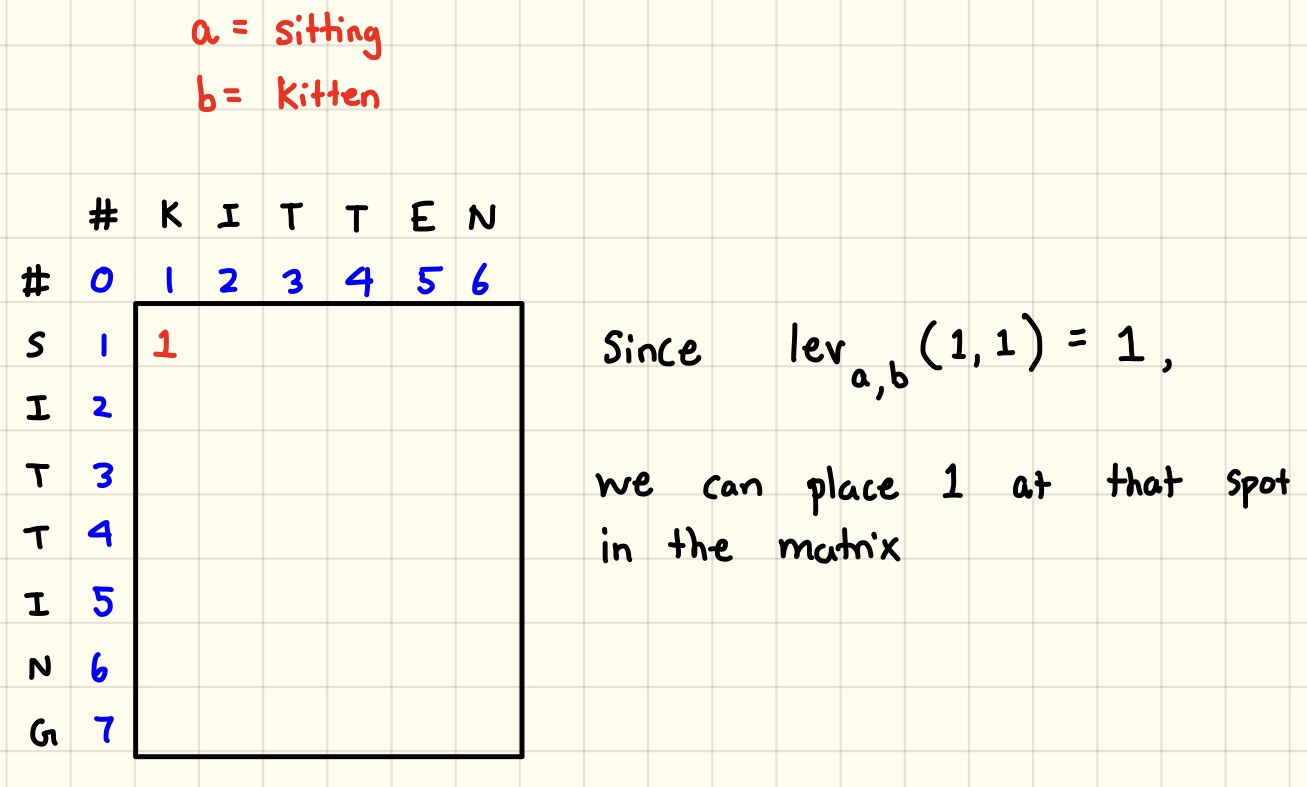
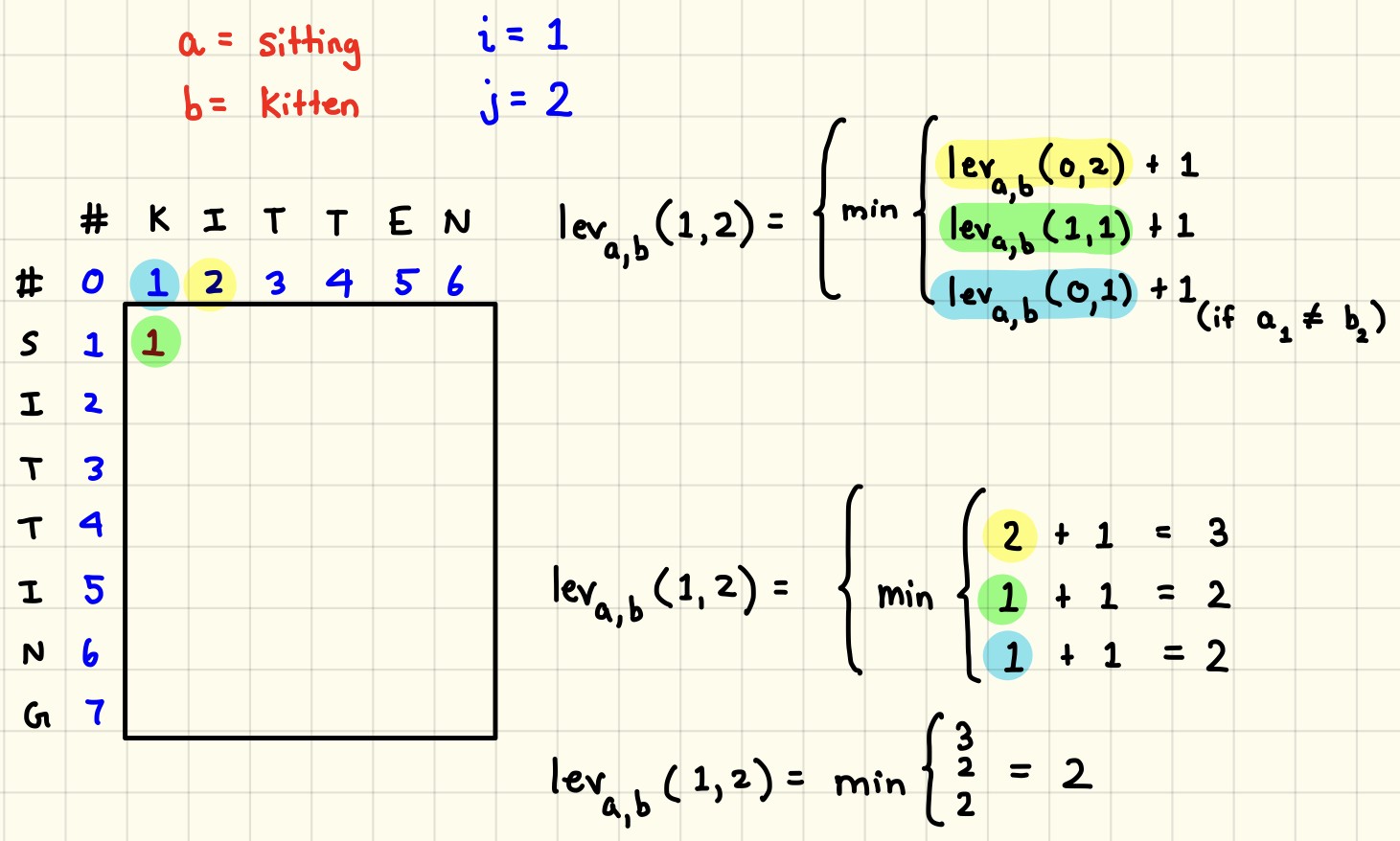
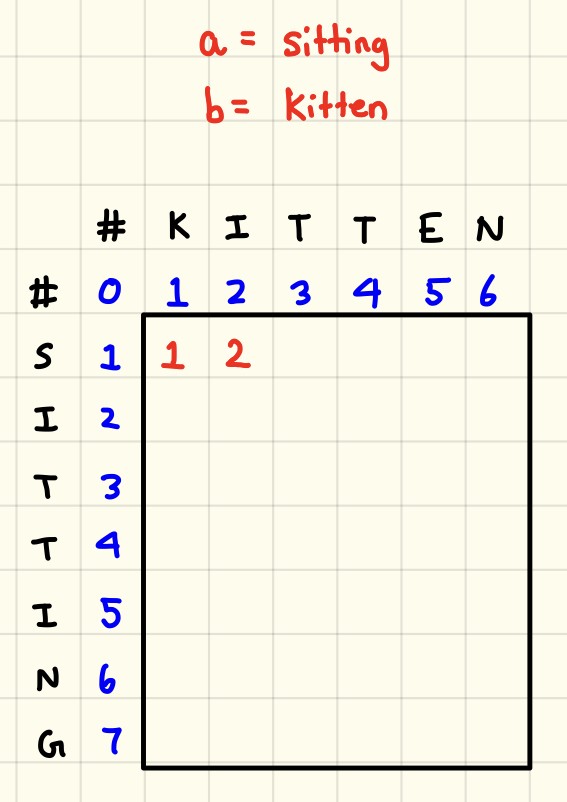
- Levenshtein distance
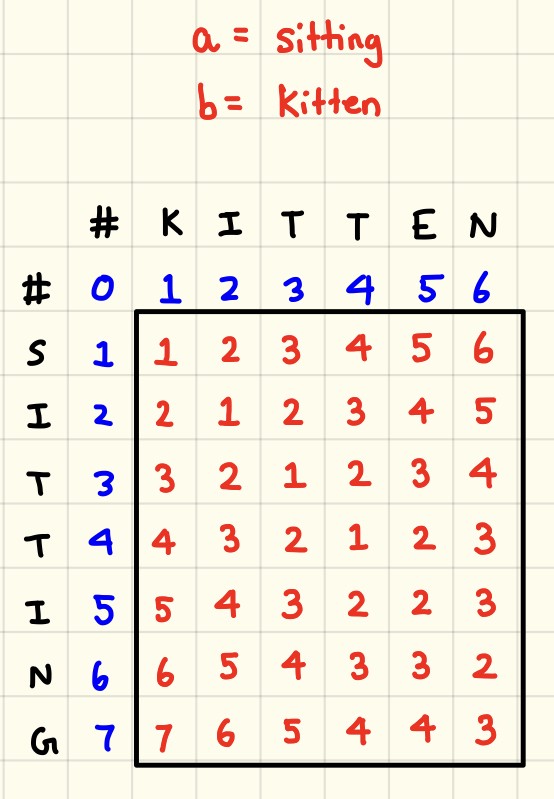
- One of edit distance based algorithms which is falling under this category try to compute the number of operations needed to transforms one string to another. More the number of operations, less is the similarity between the two strings. One point to note, in this case, every index character of the string is given equal importance.
- A number that tells you how different two strings are. The higher the number, the more different the two strings are.
- And 'edit' is defined by either an insertion of a character, a deletion of a character, or a replacement of a character.
- It measures the minimum number of edits that you need to do to change a one-word sequence into the other.
Reference : medium.com/@ethannam/understanding-the-levenshtein-distance-equation-for-beginners-c4285a5604f0







- User-defined function
import numpy as np
def levenshtein_ratio_and_distance(s,t,ratio_calc=False):
rows=len(s)+1
cols=len(t)+1
distance=np.zeros((rows,cols), dtype=int)
for i in range(1,rows):
for k in range(1,cols):
distance[i][0]=i
distance[0][k]=k
for col in range(1, cols):
for row in range(1, rows):
if s[row-1]==t[col-1]:
cost=0
else:
if ratio_calc==True:
cost=2
else:
cost=1
distance[row][col]=min(distance[row-1][col]+1,
distance[row][col-1]+1,
distance[row-1][col-1]+cost)
if ratio_calc==True:
Ratio=((len(s)+len(t))-distance[row][col])/(len(s)+len(t))
return Ratio
else:
return 'The strings are {} edits away'.format(distance[row][col]) s1='Apple.'
s2='apple'
Distance=levenshtein_ratio_and_distance(s1,s2)
print(Distance)
Ratio=levenshtein_ratio_and_distance(s1,s2,ratio_calc=True)
Ratio
>>>The strings are 2 edits away
>>>0.7272727272727273
s1='Apple.'
s2='apple'
Distance=levenshtein_ratio_and_distance(s1.lower(),s2.lower())
print(Distance)
Ratio=levenshtein_ratio_and_distance(s1.lower(),s2.lower(),ratio_calc=True)
Ratio
>>>The strings are 1 edits away
>>>0.9090909090909091
The first function found the 2 differences between the two strings. These were the upper/lower case and full stop at the end of the first string as well as a similarity ratio of 72%, which is pretty high.
The second function that the distance has been reduced by 1 simply by turning the strings to lower case before comparing and the similarity ratio to 90%.
- Python Levenshtein package
!pip install Levenshtein
import Levenshtein as lev
s1='APPLE.'
s2='apple'
Distance=lev.distance(s1.lower(),s2.lower())
print(Distance)
Ratio=lev.ratio(s1.lower(),s2.lower())
print(Ratio)
>>>1
>>>0.9090909090909091In the user-defined function above, when the similarity ratio is calculated, the cost of a substitution is 2 instead of 1. That is because lev.ratio() assigns such a cost for a substitution.
Reference : www.datacamp.com/community/tutorials/fuzzy-string-python
import textdistance
textdistance.levenshtein('apple', 'APPLE.')
>>>6
textdistance.levenshtein.normalized_similarity('text', 'test')
>>>0.75The two strings vary all the positions, hence the edit distance is 6. It distinguishes a capital letter and a small letter.
One thing to note is the normalized similarity, this is a function to bound the edit distance between 0 and 1. This signifies, a score of 1 is for a perfect match. So the strings are 75% similar.
Reference : itnext.io/string-similarity-the-basic-know-your-algorithms-guide-3de3d7346227
'Analyze Data > Measure of similarity' 카테고리의 다른 글
| Vector Similarity-2. Euclidean distance (0) | 2021.03.03 |
|---|---|
| Vector Similarity-7. Sørensen similarity (0) | 2021.03.02 |
| Vector Similarity-3. Jaccard Similarity (0) | 2021.03.02 |
| Vector Similarity-6. Jaro-Winkler distance (0) | 2021.03.02 |
| Vector Similarity-5. Jaro distance (0) | 2021.02.26 |