Logistic Regression, Sigmoid function

• Logistic Regression

 

The problem that determines one of the two is called binary classification. And there is logistic regression for solving binary classification. It has a single layer of weights.

 

To represent these problems, we need functions that can be represented in the S-shape rather than a straight-line function such as Wx + b(

2021.03.16 - [Machine Learning] - Linear Regression, Simple Linear Regression, Multiple Linear Regression, MSE, Cost function, Loss function, Objective function, Optimizer, Gradient Descent

). If you use straight lines for these problems, the classification process does not work well.

 

So this logistic regression hypothesis is not \(H(x) = Wx + b\) for linear regression, but we're going to use the hypothesis of \(H(x) = f(Wx + b)\) using some particular function \(f\) that can create an S-shaped graph.

 

x : given data y : result of x  If result(y) has given, what result H(x) will get?

 

• Sigmoid function

 

The functions that can be represented in the S-shape.

 

---

If you draw a graph in the above data, if you say pass is 1 and fail is 0, it is as follows(S-shape).

 

---

---

e(Euler's number)=2.718281...

 

---

1. If W=1, b=0 (original : σ(Wx+b))

 

%matplotlib inline
import numpy as np 
import matplotlib.pyplot as plt

def sigmoid(x):
  return 1/(1+np.exp(-x))
x = np.arange(-5.0, 5.0, 0.1)
y=sigmoid(x)

plt.plot(x,y,'g')
plt.plot([0,0],[1.0,0.0],':')
plt.show()

As a result, sigmoid turns out between 0 and 1

If x=0, σ(sigmoid)=0.5

If x increasing, it converges to 0

---

2. If W=0.5, 1, 2, b=0 

 

def sigmoid(x):
  return 1/(1+np.exp(-x))
x=np.arange(-5.0,5.0,0.1)
y1=sigmoid(0.5*x)
y2=sigmoid(x)
y3=sigmoid(2*x)

plt.plot(x,y1, 'r', linestyle='--')
plt.plot(x,y2,'g')
plt.plot(x,y3,linestyle='--')
plt.plot([0,0],[1.0,0.0],':')
plt.show()

 

In linear regression, the weight 'W' was meant to be the slope of the straight line(

2021.03.16 - [Machine Learning] - Linear Regression, Simple Linear Regression, Multiple Linear Regression, MSE, Cost function, Loss function, Objective function, Optimizer, Gradient Descent

), but here the weight 'W' determines the slope of the graph.

Increasing W, steeper slope. Vice versa.

---

3. If W=1, b=0.5, 1, 2

 

def sigmoid(x):
  return 1/(1+np.exp(-x))
x=np.arange(-5.0,5.0,0.1)
y1=sigmoid(x+0.5)
y2=sigmoid(x+1)
y3=sigmoid(x+1.5)

plt.plot(x,y1, 'r', linestyle='--')
plt.plot(x,y2,'g')
plt.plot(x,y3,linestyle='--')
plt.plot([0,0],[1.0,0.0],':')
plt.show()

 

The above graph shows the graph moving left and right depending on the value of b.

---

4. Simple Logistic Regression

 

Hypothesis : y is 1 if x is over 10, otherwise y is 0.

import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt 
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras import optimizers

X=np.array([-50, -40, -30, -20, -10, -5, 0, 5, 10, 20, 30, 40, 50])
y=np.array([0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1])

model=Sequential()
model.add(Dense(1,input_dim=1, activation='sigmoid'))

opt=optimizers.SGD(lr=0.01)
model.compile(optimizer=opt, loss='binary_crossentropy', metrics=['binary_accuracy'])
model.fit(X,y,batch_size=1, epochs=30, shuffle=False)
>>>
...

Epoch 29/30
13/13 [==============================] - 0s 1ms/step - loss: 0.1125 - binary_accuracy: 0.9526
Epoch 30/30
13/13 [==============================] - 0s 2ms/step - loss: 0.1117 - binary_accuracy: 0.9526

plt.plot(X,model.predict(X), 'b', X,y,'k.')

model.predict([1,2,3,4,5,10,11,12,13,14])
>>>
array([[0.45559546],
       [0.5141264 ],
       [0.57227236],
       [0.6284881 ],
       [0.6814285 ],
       [0.87362355],
       [0.89733815],
       [0.9170253 ],
       [0.9332182 ],
       [0.9464355 ]], dtype=float32)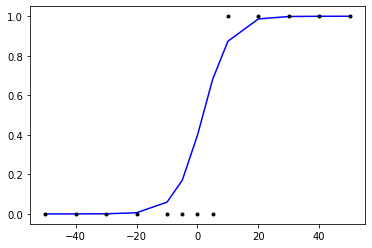

---

5. Multiple Logistic Regression

 

Hypothesis : y is 0 if x is 0, otherwise 1 if there is 1 in x.

X=np.array([[0,0],[0,1],[1,0],[1,1]])
y=np.array([0,1,1,1])

from tensorflow.keras.models import Sequential 
from tensorflow.keras.layers import Dense 
from tensorflow.keras import optimizers

model=Sequential()
model.add(Dense(1, input_dim=2, activation='sigmoid'))
model.compile(optimizer='sgd',loss='binary_crossentropy', metrics=['binary_accuracy'])
model.fit(X,y,batch_size=1, epochs=40, shuffle=False)
>>>
...
4/4 [==============================] - 0s 3ms/step - loss: 0.5540 - binary_accuracy: 0.5333
Epoch 400/400
4/4 [==============================] - 0s 2ms/step - loss: 0.5534 - binary_accuracy: 0.5333

model.predict(X)
>>>
array([[0.626424  ],
       [0.8194542 ],
       [0.82448316],
       [0.9270863 ]], dtype=float32)

Ecxept for [0,0], rest of pairs got close to 1.

---

• Logistic Regression Cost function

 

The feature of Sigmoid function is that the output of this function is between 0 and 1.

 

 

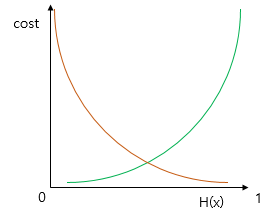
- Orange line : When the real value is 1

- Green lin : When the real value is 0

---

---

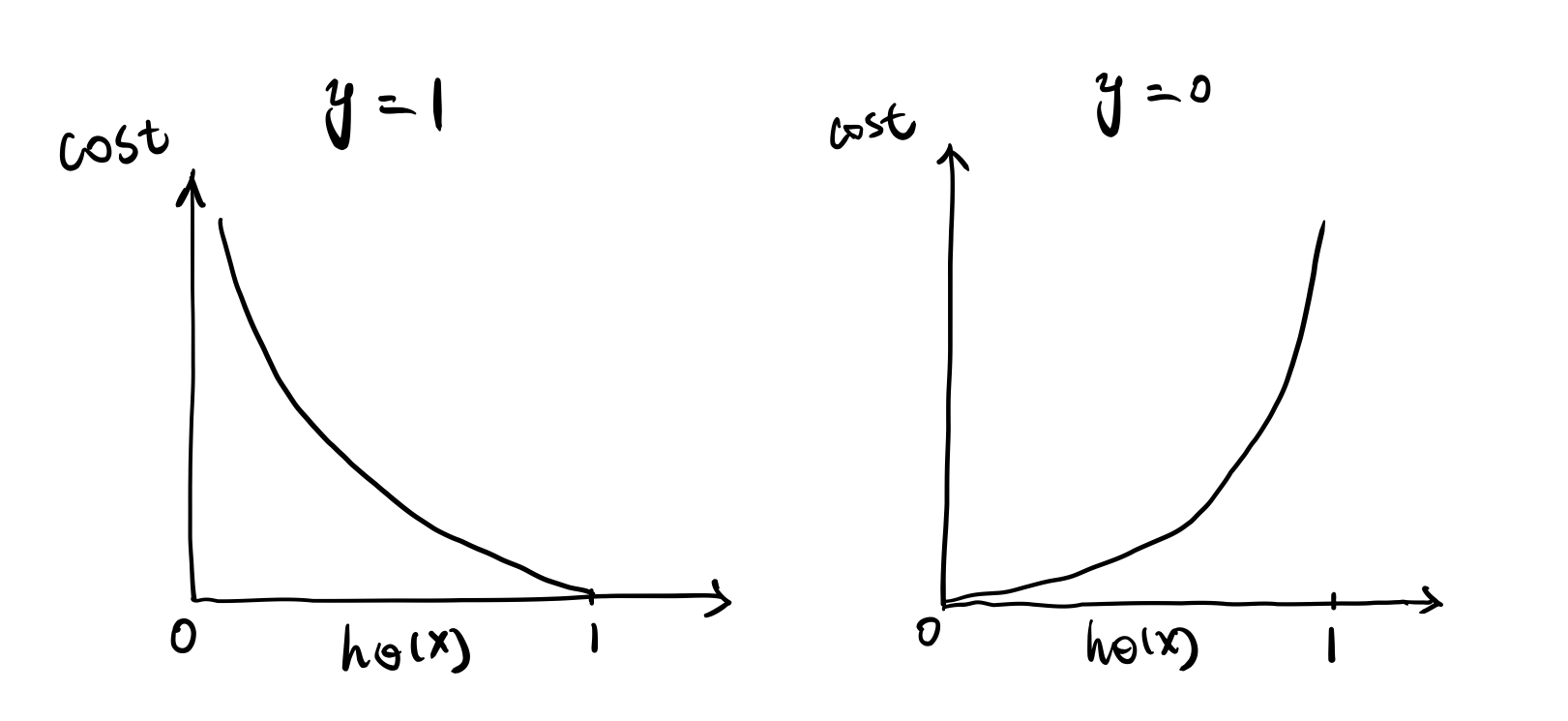
0<y<1 Less than 0.5 is considered 0 More than 0.5 is considered 1

 

If y(result) is 1, the prediction is 1, then the cost is 0.

If y(result) is 1, the prediction is 0, then this is totally opposite prediction, so the learning algorithm is punished by a very large cost. 

Vice versa.

Reference : towardsdatascience.com/optimization-loss-function-under-the-hood-part-ii-d20a239cde11

---

- If combine the two equations into one equation,

\( \text{cost}(H(x), y) = -\left[ y \log\bigl(H(x)\bigr) + (1 - y)\log\bigl(1 - H(x)\bigr) \right] \)

- Then, get the average of all errors,

\( \mathrm{cost}(W) = -\frac{1}{n} \sum_{i=1}^{n} \left[ y^{(i)} \log H\!\left(x^{(i)}\right) + \left(1 - y^{(i)}\right) \log \left(1 - H\!\left(x^{(i)}\right)\right) \right] \)

 

losses = -(y_train * torch.log(hypothesis) + 
           (1 - y_train) * torch.log(1 - hypothesis))
           
cost = losses.mean()
print(cost)

 

The code above is same as folow.

import torch.nn.functional as F

F.binary_cross_entropy(hypothesis, y_train)

 

https://wikidocs.net/57805