Softmax Regression, Cross Entropy

• Softmax Regression(Multi-class Classification)

 

Multi-Class Classification to choose one from three or more options.

 

• Softmax function

 

It applies this idea to the multi-class classification problem, where the sum of the probabilities is 1, not like a binary classification(2021.03.16 - [Machine Learning] - Linear Regression, Simple Linear Regression, Multiple Linear Regression, MSE, Cost function, Loss function, Objective function, Optimizer, Gradient Descent).

 

Let the sum of all probabilities be 1 and change it to probability.

---

---

\( H(X) = \operatorname{softmax}(WX + B) \)

---

\( p_i = \frac{e^{z_i}}{\sum_{j=1}^{k} e^{z_j}}, \quad \text{for } i = 1, 2, \ldots, k \)

Then,

\( \operatorname{softmax}(\mathbf{z}) = \left[ \frac{e^{z_1}}{\sum_{j=1}^{3} e^{z_j}}, \frac{e^{z_2}}{\sum_{j=1}^{3} e^{z_j}}, \frac{e^{z_3}}{\sum_{j=1}^{3} e^{z_j}} \right] = [p_1, p_2, p_3] = \hat{\mathbf{y}} \quad \text{(예측값)} \)

---

 

⬇︎

 

 

⬇︎

 

⬇︎

 

⬇︎

 

⬇︎

 

⬇︎

 

---

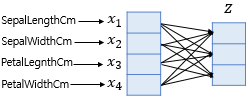
Example 1.

 

---

---

---

---

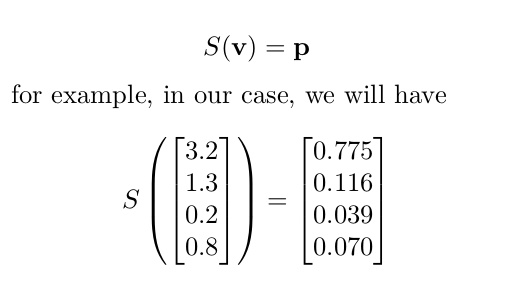Example 2.

 

Choose one of the three.

 

SepalLengthCm()	SepalWidthCm()	PetalLengthCm()	PetalWidthCm()	Species(y)
5.1	3.5	1.4	0.2	setosa
4.9	3.0	1.4	0.2	setosa
5.8	2.6	4.0	1.2	versicolor
6.7	3.0	5.2	2.3	virginica
5.6	2.8	4.9	2.0	virginica

---

\( X = \begin{pmatrix} x_{11} & x_{12} & x_{13} & x_{14} \\ x_{21} & x_{22} & x_{23} & x_{24} \\ x_{31} & x_{32} & x_{33} & x_{34} \\ x_{41} & x_{42} & x_{43} & x_{44} \\ x_{51} & x_{52} & x_{53} & x_{54} \end{pmatrix} \), \( \hat{Y} = \begin{pmatrix} y_{11} & y_{12} & y_{13} \\ y_{21} & y_{22} & y_{23} \\ y_{31} & y_{32} & y_{33} \\ y_{41} & y_{42} & y_{43} \\ y_{51} & y_{52} & y_{53} \end{pmatrix} \), \( \mathbf{W} = \begin{pmatrix} w_{11} & w_{12} & w_{13} \\ w_{21} & w_{22} & w_{23} \\ w_{31} & w_{32} & w_{33} \\ w_{41} & w_{42} & w_{43} \end{pmatrix} \), \( B = \begin{pmatrix} b_1 & b_2 & b_3 \\ b_1 & b_2 & b_3 \\ b_1 & b_2 & b_3 \\ b_1 & b_2 & b_3 \\ b_1 & b_2 & b_3 \end{pmatrix} \)

Then,

\( \hat{Y} = \operatorname{softmax}(XW + B) \)

can be

\( \begin{pmatrix} y_{11} & y_{12} & y_{13} \\ y_{21} & y_{22} & y_{23} \\ y_{31} & y_{32} & y_{33} \\ y_{41} & y_{42} & y_{43} \\ y_{51} & y_{52} & y_{53} \end{pmatrix} = \operatorname{softmax} \Bigg( \begin{pmatrix} x_{11} & x_{12} & x_{13} & x_{14} \\ x_{21} & x_{22} & x_{23} & x_{24} \\ x_{31} & x_{32} & x_{33} & x_{34} \\ x_{41} & x_{42} & x_{43} & x_{44} \\ x_{51} & x_{52} & x_{53} & x_{54} \end{pmatrix} \begin{pmatrix} w_{11} & w_{12} & w_{13} \\ w_{21} & w_{22} & w_{23} \\ w_{31} & w_{32} & w_{33} \\ w_{41} & w_{42} & w_{43} \end{pmatrix} + \begin{pmatrix} b_1 & b_2 & b_3 \\ b_1 & b_2 & b_3 \\ b_1 & b_2 & b_3 \\ b_1 & b_2 & b_3 \\ b_1 & b_2 & b_3 \end{pmatrix} \Bigg) \)

 

---

• Softmax Cost function(Cross Entropy)

 

Softmax regression uses a cross entropy function as a cost function.

---

	Cost function
Linear Regression	MSE(Mean Squared Error)	2021.03.16 - [Machine Learning] - Linear Regression, Simple Linear Regression, Multiple Linear Regression, MSE, Cost function, Loss function, Objective function, Optimizer, Gradient Descent
Logistic Regression	H(x) = sigmoid(Wx + b)	2021.03.17 - [Machine Learning] - Logistic Regression, Sigmoid function
Softmax Regression(Multi-class Classification)	Softmax Cost function(Cross Entropy)	2021.03.31 - [Machine Learning] - Entropy, Cross-Entropy

---

import torch.nn.functional as F

z=torch.rand(3,5, requires_grad=True)
hypothesis=F.softmax(z, dim=1)

 

tensor z with shape (3, 5):

---

dim = 0 (across rows/column-wise):

 

- Softmax is applied down each column

- Each of the 5 columns will sum to 1

- You're normalizing the 3 values within each column

z = [[a, b, c, d, e],
     [f, g, h, i, j],
     [k, l, m, n, o]]
     
# Column 0: softmax([a,f,k]) → sums to 1
# Column 1: softmax([b,g,l]) → sums to 1
# ... and so on

---

dim = 1 (across columns/row-wise):

 

- Softmax is applied across each row

- Each of the 3 rows will sum to 1

- You're normalizing the 5 values within each row

- dim=1 is typical for classification where each row is a sample and columns are class scores

z = [[a, b, c, d, e],    # Row 0: softmax([a,b,c,d,e]) → sums to 1
     [f, g, h, i, j],    # Row 1: softmax([f,g,h,i,j]) → sums to 1  
     [k, l, m, n, o]]    # Row 2: softmax([k,l,m,n,o]) → sums to 1

 

https://wikidocs.net/59427

towardsdatascience.com/softmax-activation-function-how-it-actually-works-d292d335bd78