Kalman Filter

• Kalman Filter

 

 

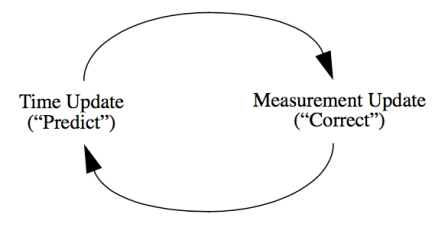
It works by a two-phase process having a prediction phase and an update phase.

- For the prediction phase, the Kalman filter produces estimates of the current state variables, along with their uncertainties.

- Once the outcome of the next measurement (necessarily corrupted with some error, including random noise) is observed, these estimates are updated using a weighted average, with more weight being given to estimates with greater certainty.

- The algorithm is recursive. It can operate in real time, using only the present input measurements and the state calculated previously and its uncertainty matrix; no additional past information is required.

 

Conditions If the motion model and the measurement model are linear. If the motion model and the measurement model follow a Gaussian distribution.

---

• Prediction phase

Predict the current state distribution.

 

 

- μ : Average of probability distribution

- σ : Distribution of of probability distribution

---

• Update phase

 

Update posterior probability distribution.

 

- Example

 

1) Prior Belief

 

Prior Gaussian distribution

 

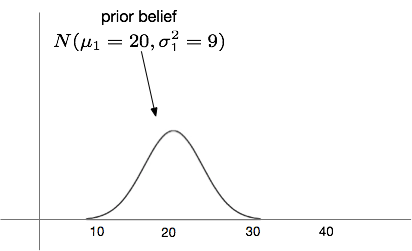
- μ1 : Suppose that the robot was 20 meters away.

- σ1 : Distribution

 

2) Current Belief

 

Updated Gaussian distribution

 

- μ2 : The Sensor measured that the robot is 30 meters.

- σ2 : Distribution

 

3) Updated Gaussian Probability Distribution

 

 

↓

 

 

∴

 

 

https://soohwan-justin.tistory.com/42

https://medium.com/@celinachild/kalman-filter-%EC%86%8C%EA%B0%9C-395c2016b4d6

https://gaussian37.github.io/ad-ose-lkf_basic/

https://codingcoding.tistory.com/439