- Bayes Filter
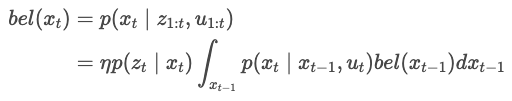
It can be divided into a Prediction Step and a Correction Step.
- Prediction Step
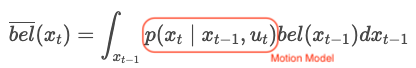
The state of prediction step.
It is a process of estimating the probability of the current robot state using control input data () and robot state of previous step (). is call a Motion Model because it estimates the robot's movement by input () and calculates the probability of the current state.- Motion Model

Higher Certainty : The more distributed or darker the spots.
Distributed well.
The uncertification of the direction of progress is greater.
The uncertification of the rotation is greater than the direction.
A Posterior Probability that the control input () will change the previous state () to the current state ().
It can be divided into an Odometry-based Model and a Velocity-based Model.
- Odometry-based Model
Model using sensor data of wheel encoder on robot or car wheels. More accurate than Velocity Model.
- Velocity-based Model
Model using an inertial sensor such as IMU. It mainly used when odometry models are not available.
- Correction Step
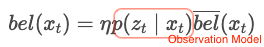
It is a step of predicting the current position of the robot using input data () and correcting the predicted position of the robot from the sensor data () obtained at that position. is refferred to as an Observation Model, and means the probability that the sensor data () obtained from the currently predicted state ().
- η : Normalization
normalizer = 1 / (Sum of all the likelihood vectors)
To turn likelihood into a probability distribution function, we need to adjust the scale by multiplying the fixed scale factor so that the sum of each value is 1.
When the robot detects light, it has a value that is three times greater than when it does not. We call this scale factor to a normalizer.
For instance,
likelihood = [1,3,1,3,1,1,1,3,1,1]
1+3+1+3+1+1+1+3+1+1 = 16
1/16 = 0.0625
∴ normalized_likelihood = [0.0625,0.1875,0.0625,0.1875,0.0625,0.0625,0.0625,0.1875,0.0625,0.0625]
def normalize(inputList):
""" calculate the normalizer, using: (1 / (sum of all elements in list)) """
normalizer = 1 / float(sum(inputList))
# multiply each item by the normalizer
inputListNormalized = [x * normalizer for x in inputList]
return inputListNormalized- Observation Model
The probability of sensor data in the current state.
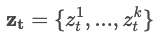
- : Data group vector - ~ : Each scan data in each t step.
- Observation
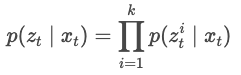
Multiplication of the probabilities of each sensor data in the current state.
- ∏ : Product(Multiplication)
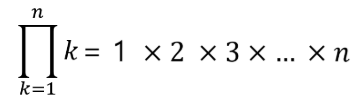
For instance,
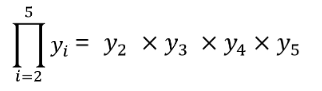
https://jinyongjeong.github.io/2017/02/14/lec02_motion_observation_model/
'Autonomous Vehicle > Theory' 카테고리의 다른 글
| (prerequisite-Poisson distribution) Binomial Distribution (0) | 2024.03.15 |
|---|---|
| Kalman Filter (0) | 2024.03.14 |
| (prerequisite-Kalman Filter) Bayes' Theorem(Baysianism) (0) | 2024.03.13 |
| Probability Distribution, Random Variable, Probability Function, Cumulative Distribution Function (0) | 2024.03.13 |
| (prerequisite-Kalman Filter) State Equation, Measurement Equation (0) | 2024.03.06 |