| Probability Distribution | Random Variable | Probability Function |
|
| Discrete Probability Distribution | Discrete Probability Variable | Probability Mass Function(PMF) | Cumulative Distribution Function(CDF) |
| Continuous Probability Distribution | Continuous Probability Variable | Probability Density Function(PDF) | |
- Probability Distribution
It is the mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment.
For instance, if X is used to denote the outcome of a coin toss ("the experiment"), then the probability distribution of X would take the value 0.5 (1 in 2 or 1/2) for X = heads, and 0.5 for X = tails.
This is divided into two parts.
- Discrete Probability Distribution
- Continuous Probability Distribution
- Feature of Probability Distribution
- The probability is between 0 and 1.
- The sum of the sample spaces is 1.
- The probability in any interval is the sum of everything in that interval.
- Random Variable
A variable represented by quantifying the results that may occur in a specific probability experiment.
- Discrete Random Variable : The values that can have are countable, such as the number of defective products, the number of accidents.
- Probability Function
It receives the Random Variable as an input and outputs the probability that the value will appear.
- Probability Mass Function(PMF) for Discrete Probability Distribution
- Probability Density Function(PDF) for Continuous Probability Distribution
- Probability Mass Function(PMF)
- Expression

or

The function that presents the probability for a particular value in Discrete Random Variable.
- Example
1) Throwing 3 coins
2) 8 times in total
3) The number of head : 0, 1, 2, 3
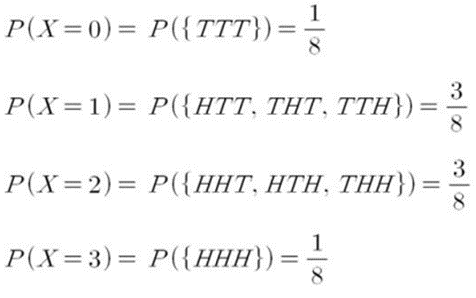
4) Probability Mass Function(PMF) of Throwing 3 coins

5) Probability Mass Function(PMF) of Y
Y : The difference in the number of Head and Tail, it has 1, 3.
TTT : 3-0=3
HTT : 2-1=1
THT : 2-1=1
...

- Feature of Probability Mass Function(PMF)

- Cumulative Distribution Function(CDF)
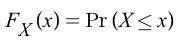
A function whose result is the probability that the random variable X accumulates from -∞ to a specific point (input).
input : x
output <=x
- CDF in Discrete Probability Variable
- X : A number that comes out of a roll of a dice
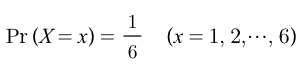
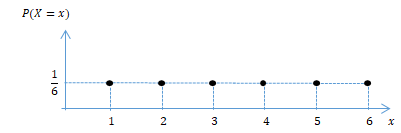
- CDF Graph of X

- CDF Function of X

[X] is an integer not bigger than x.
- CDF in Continuous Probability Variable

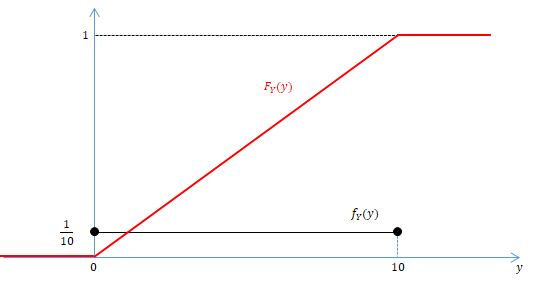
- Y : The time waiting for the bus that is supposed to be arrived in 10 mins.
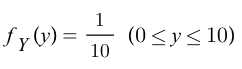
- Y CDF

- CDF Graph of Y
- Fearues of CDF
- The larger the input, the output is greater than input or equal.
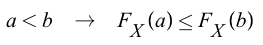
if a<b
Pr(X < a) ≤ Pr(X < b)- The smaller the input, the closer the accumulated probability is to zero, and the larger the input, the closer the cdf value is to 1(because it accumulates probabilities for most ranges taken by X).

∴
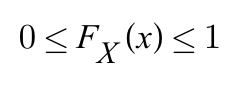
- Right Continuous

'Autonomous Vehicle > Theory' 카테고리의 다른 글
| Kalman Filter (0) | 2024.03.14 |
|---|---|
| Prediction Step, Motion Model, Correction Step, Observation Model (0) | 2024.03.14 |
| (prerequisite-Kalman Filter) Bayes' Theorem(Baysianism) (0) | 2024.03.13 |
| (prerequisite-Kalman Filter) State Equation, Measurement Equation (0) | 2024.03.06 |
| (prerequisite-Kalman Filter) Localization, Tracking (0) | 2023.07.06 |