Null Space

• Null Space

 

In the linear equation Ax=b, when b is a zero vector (=Null vector or 0 vector), it is a set of all possible solutions x that satisfy the equation.

 

Null Space of A = all solutions $x=\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]\mathrm{to}\mathrm{Ax}=0$

---

For example, there is an equation

$Ax=\left[\begin{array}{ccc}1& 1& 2\\ 2& 1& 3\\ 3& 1& 4\\ 4& 1& 5\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\right]$

---

The solution of the equation above is

, or

, or

$\mathbf{\text{x}}=c\left[\begin{array}{cc}& 1\\ & 1\\ & -1\end{array}\right]$.

---

Any null space must include a zero vector.

This null space is a subspace of a 3-dimensional space.

---

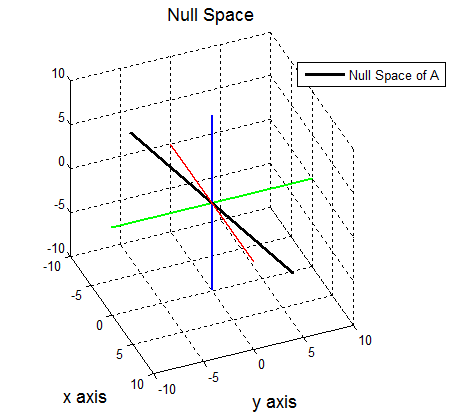
When b has an arbitrary value such as below, does solution x form a vector space?

 

$Ax=\left[\begin{array}{ccc}1& 1& 2\\ 2& 1& 3\\ 3& 1& 4\\ 4& 1& 5\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]=\left[\begin{array}{c}1\\ 2\\ 3\\ 4\end{array}\right]$

 

No, because there is no zero vector in the solution. In other words, it does not pass the origin. If b is a nonzero vector, there may be a plane or line for any solution, but they do not pass the origin. Therefore, there is no vector space for a solution for any nonzero vector b.

 

https://twlab.tistory.com/17