- 2D Transformations
A method used to model the matching relationship between two images directly on a 2D plane.
- Rigid Transformation(Euclidean transformation)
Only change its position and orientation while maintaining its shape and size.
In other words, it is a transformation that only allows rotation and translation.
- Translation
\begin{equation}t_{x}=\frac{1}{n}\sum_{i}\left(x_{i}^{\prime}-x_{i}\right)\end{equation} \begin{equation}t_{y}=\frac{1}{n}\sum_{i}\left(y_{i}^{\prime}-y_{i}\right)\end{equation}
- Degree of Freedom(DOF) : t1, t2
- Shearing
If you want to scale the figure image on the left side by a multiple of the horizontal and vertical b times as shown on the right side, you can apply x'=ax and y' = bx.
- Rotation
- A transformation matrix that rotates (x, y) counterclockwise by θ radian. The object is spinning based on (0,0).
- Degree of Freedom(DOF) : 1, therefore, only one matching pair can determine the rotational transformation.
\begin{equation}\left.\left[\begin{array}{c}x'\\y'\end{array}\right.\right]= \left[\begin{array}{cc}\cos\theta&-\sin\theta\\\ sin\theta&\cos\theta\end{array}\right] \left[\begin{array}{c}x\\y\end{array}\right]\end{equation}
- considering scale change
\begin{equation}[\begin{matrix}x'\\y'\end{matrix}]=[\begin{matrix}a&-b\\b&a\end{matrix}][\begin{matrix}x\\y\end{matrix}]\end{equation}
- Euclidean
- Degree of Freedom(DOF) :
- Rigid
Translation + Rotation
Rotate by θ around the origin of the image and then move in parallel to the original position.
The degree of freedom of the rotational transformation is 3. It requires at least 2 matching pairs.
\begin{equation}\left[\begin{array}{c}x'\\y'\end{array}\right] =\left[\begin{array}{cc}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{array}\right]\left[\begin{array} {c}x\\y\end{array}\right]+\left[\begin{array}{c}c\\d\end{array}\right]\end{equation} c : tx + rotation d : ty + rotation [tx, ty] : translation
- Similarity
- Degree of Freedom(DOF) :
\begin{equation}[\begin{matrix}x'\\y'\end{matrix}]= [\begin{matrix}a&-b\\b&a\end{matrix}][\begin{matrix}x\\y\end{matrix}]+[\begin{matrix}c\\d\end{matrix}]\end{equation}
- Convert to homogeneous coordinate system
In order to be a single matrix from Rotation + Translation + Scaling
\begin{equation}\left.\left[\begin{array}{c}x'\\y'\\1\end{array}\right.\right]=\left[\begin{array}{ccc}a&-b&c\\b&a&d\\0&0&1\end{array}\right]\left[\begin{array}{c}x\\y\\1\end{array}\right]\end{equation}
- Affine Transformation
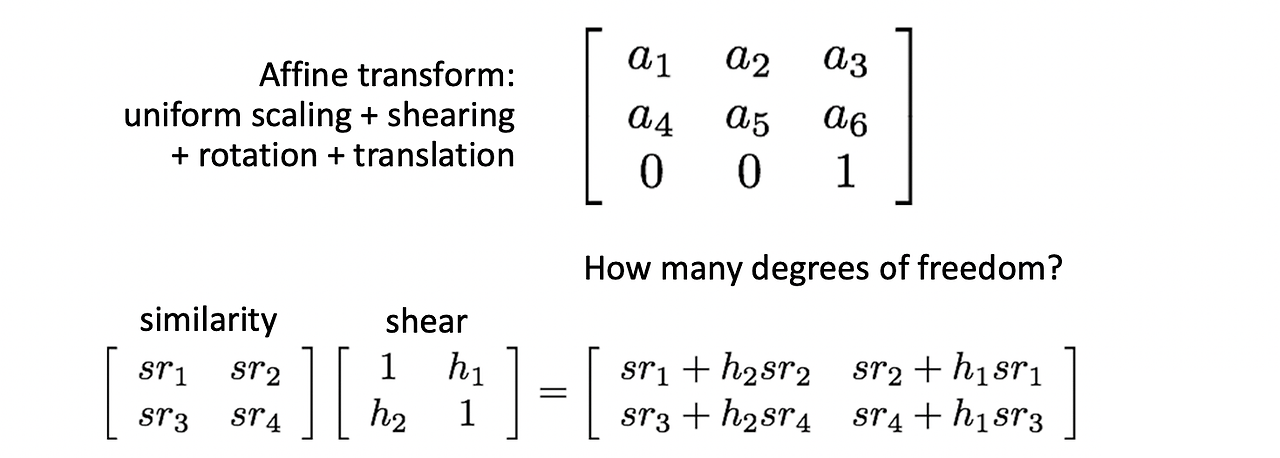
- A transformation that preserves linearity, length (distance) ratio, and parallelism.
- Degree of Freedom(DOF) : 6, +
\begin{equation}\left.\left[\begin{array}{c}x'\\y'\end{array}\right.\right]=\left[\begin{array}{cc}a&b\\c&d\end{array}\right]\left[\begin{array}{c}x\\y\end{array}\right]+\left[\begin{array}{c}e\\f\end{array}\right]\end{equation}
- Convert to homogeneous coordinate system
\begin{equation}\left[\begin{array}{c}x'\\y'\\1\end{array}\right]=\left[\begin{array}{cc}a&b&e\\c&d&f\\0&0&1\end{array}\right]\left[\begin{array}{c}x\\y\\1\end{array}\right]\end{equation}
- Homograpy (Projective Transformation)
If a planar surface is projected as an image A and an image B for different camera positions, the relationship between the image A and the image B may be expressed as a homography.
\begin{equation}\left.w\left[\begin{array}{c}x'\\y'\\1\end{array}\right.\right]=\left[\begin{array}{c}h_{11} h_{12} h_{13}\\h_{21} h_{22} h_{23}\\h_{31} h_{32} h_{33}\end{array}\right]\left[\begin{array}{c}x\\y\\1\end{array}\right]\end{equation}
https://velog.io/@richpin/Computer-Vision-07-2D-Transformations
'Autonomous Vehicle > Video Geometry' 카테고리의 다른 글
| Homography (0) | 2024.07.25 |
|---|---|
| Camera Calibration (0) | 2024.07.23 |
| 3D Transformations (0) | 2024.07.19 |
| Coordinate System (0) | 2024.07.18 |
| Epipolar Geometry (0) | 2023.09.11 |