- Transformation matrix
Rotation and parallel translation only in 3D Transformations(not like a 2D Transformations).
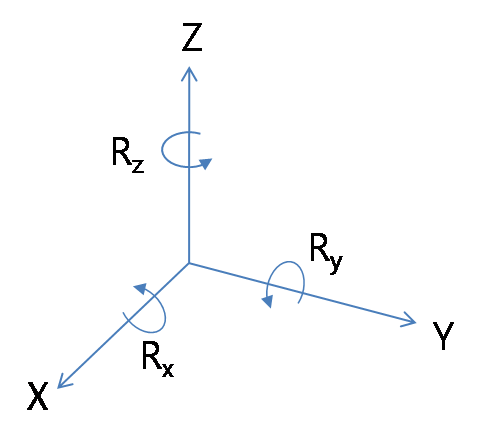
A matrix that rotates points (X, Y, Z) in a 3D space by θ radians based on the X, Y, and Z axes.
\begin{equation}\begin{gathered} R_{x}(\theta)= \left.\left[\begin{array}{cc}{1}&{0}&{0}\\{0}&{\cos\theta}&{-\sin\theta}\\{0}&{\sin\theta}&{\cos\theta}\end{array}\right.\right] \\ R_{y}(\theta)= \left.\left[\begin{array}{ccc}{\cos\theta}&{0}&{\sin\theta}\\{0}&{1}&{0}\\{-\sin\theta}&{0}&{\cos\theta}\end{array}\right.\right] \\ R_{z}(\theta)= \left.\left[\begin{array}{ccc}{\cos\theta}&{-\sin\theta}&{0}\\{\sin\theta}&{\cos\theta}&{0}\\{0}&{0}&{1}\end{array}\right.\right] \end{gathered}\end{equation}
\begin{equation}R{=}R_z(\theta_3)R_y(\theta_2)R_x(\theta_1)\end{equation}
- 3D Transformation matrix(Rigid Transformation)
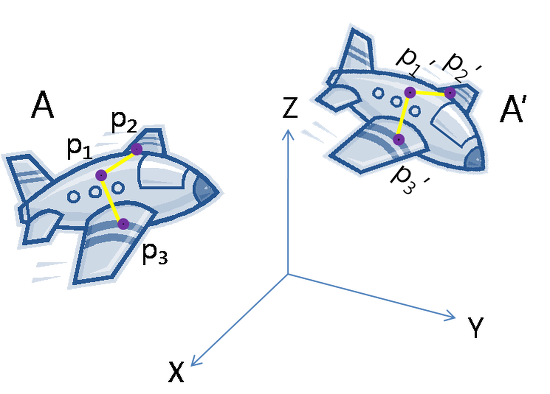
\begin{equation}\begin{bmatrix}X'\\Y'\\Z'\end{bmatrix}=R\begin{bmatrix}X\\Y\\Z\end{bmatrix}+\begin{bmatrix}t_x\\t_y\\t_z\end{bmatrix}\end{equation}
- Convert to homogeneous coordinate system
\begin{equation}\begin{bmatrix}X'\\Y'\\Z'\\1\end{bmatrix}=\begin{bmatrix}r_{11} r_{12} r_{13} t_x\\r_{21} r_{22} r_{23} t_y\\r_{31} r_{32} r_{33} t_z\\0\quad0\quad0\quad1\end{bmatrix}\begin{bmatrix}X\\Y\\Z\\1\end{bmatrix}\end{equation}
'Autonomous Vehicle > Video Geometry' 카테고리의 다른 글
| Homography (0) | 2024.07.25 |
|---|---|
| Camera Calibration (0) | 2024.07.23 |
| 2D Transformations (0) | 2024.07.19 |
| Coordinate System (0) | 2024.07.18 |
| Epipolar Geometry (0) | 2023.09.11 |