Camera Calibration

---

The tree(3D) ←→ Camera(2D)

 

The tree : The point we're seeing with our eyes, 3D point which has world coordinate

Camera : When we take the tree, it transforms to 2D

---

 

3D Projection Geometry:

• The camera is at point C (camera center).
• A 3D point in space is projected through the pinhole onto the image plane.
• The image plane is in front of the camera in this drawing, which is a convention to avoid flipping.

---

 

2D Side View:

• Shows that a point at depth Z gets projected a distance f·X/Z (or f·Y/Z) from the center of the image plane, where f is the focal length.

---

 

Basic Projection:$$(X,Y,Z{)}^T\mapsto {(\frac{fX}{Z},\frac{fY}{Z})}^T$$

---

Matrix Form:$$\left(\begin{array}{c}x\\ y\end{array}\right)=\left(\begin{array}{ccc}f& 0& 0\\ 0& f& 0\end{array}\right)\left(\begin{array}{c}\frac{X}{Z}\\ \frac{Y}{Z}\\ 1\end{array}\right)$$

---

Homogeneous coordinates:$$\lambda \left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=\left[\begin{array}{cccc}f& 0& 0& 0\\ 0& f& 0& 0\\ 0& 0& 1& 0\end{array}\right]\left[\begin{array}{c}X\\ Y\\ Z\\ 1\end{array}\right]$$

---

When we take the picture of the tree, the camera influenced by the Camera intrinsic parameters-lens, the distance between the lens and the image sensor, the angle between the lens and the image sensor, etc.

 

Therefore, when finding the position where the 3D points are projected on the image or, conversely, restoring the 3D coordinates from the image coordinates, these internal factors must be removed to ensure accurate calculation.

 

And the process of finding the parameter values of these internal factors is called camera calibration.

---

$$A[R\mid t]\left[\begin{array}{c}X\\ Y\\ Z\\ 1\end{array}\right]$$

 

- X,Y,Z : 3D coordinates in the world
- [R|t] : extrinsic parameter(Rotation matrix, Translation matrix)-related to the outer space, such as the height of the camera, the orientation(fan, tilt)
- A : intrinsic camera matrix-Internal parameters of the camera itself, such as the focal length, aspect ratio, and center point of the camera

- A[R|t] : camera matrix(projection matrix)

---

• Camera intrinsic parameters

 

Focal length, Principal point, Skew coefficient.

 

fxskewcfxcx0fycy001

---

• Focal length

 

Pinhole Camera Model

---

Pinhole Model

---

 

Distance between lens center and image sensor in pixels.

---

• Principal point

 

Lens center point.

 

In the ideal case, Cx = width/2, Cy = height/2

---

 

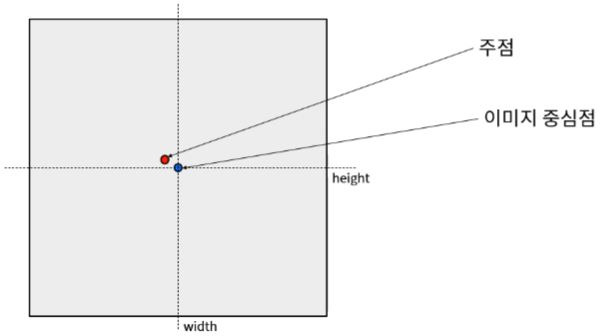
Ideally, the main point (=lens center point) matches the image center point, but there are cases where it does not match due to various issues arising from the camera manufacturing process.

---

• Skew coefficient

 

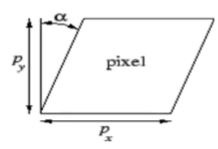
Inclined degree of y-axis.

---

 

• Camera Projection(3D to 2D)

 

We go from:$$(X,Y,Z{)}^T\in {\mathbb{R}}^3⟶(x,y{)}^T\in {\mathbb{R}}^2$$
1. 3D Point in Camera Coordinates : $${\mathbf{X}}_{\mathrm{cam}}=\left[\begin{array}{c}X\\ Y\\ Z\\ 1\end{array}\right]$$
a. Intrinsic matrix K:$$\mathbf{K}=\left[\begin{array}{ccc}f& 0& p_x\\ 0& f& p_y\\ 0& 0& 1\end{array}\right]$$
This matrix maps normalized camera coordinates to pixel coordinates:
- 𝑓: focal length (in pixels)
- p_x,p_y : principal point (usually image center)

b. Augmented identity matrix [I|0]:
$$[\mathbf{I}\mid \mathbf{0}]=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\end{array}\right]$$
This just extracts (𝑋,𝑌,𝑍) from the homogeneous 4D vector (𝑋,𝑌,𝑍,1).

3. Multiply It All Together
$${\mathbf{x}}_{\mathrm{hom}}=\mathbf{K}\cdot \left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\end{array}\right]\cdot \left[\begin{array}{c}X\\ Y\\ Z\\ 1\end{array}\right]=\mathbf{K}\cdot \left[\begin{array}{c}X\\ Y\\ Z\end{array}\right]$$
Now multiply:
$${\mathbf{x}}_{\mathrm{hom}}=\left[\begin{array}{ccc}f& 0& p_x\\ 0& f& p_y\\ 0& 0& 1\end{array}\right]\cdot \left[\begin{array}{c}X\\ Y\\ Z\end{array}\right]=\left[\begin{array}{c}fX+Z{p}_x\\ fY+Z{p}_y\\ Z\end{array}\right]$$

4. Final Summary
$${\mathbf{x}}_{\mathrm{hom}}=\mathbf{K}\cdot [\mathbf{I}\mid \mathbf{0}]\cdot {\mathbf{X}}_{\mathrm{cam}}$$

---

• Camera extrinsic parameters

 

Rotation, Translation

3D←→2D

 

These are not camera specific parameters, so they depend on where and in what direction the camera is installed and how the world coordinate system is defined.

---

• World Coordinates to Camera Coordinates (Extrinsics)

$${\mathbf{X}}_{\mathrm{cam}}=\mathbf{R}(\mathbf{X}-\mathbf{C})=\mathbf{R}\cdot \mathbf{X}+\mathbf{t}$$

This is a coordinate transformation from the world coordinate system to the camera coordinate system.

 

• X: point in the world coordinate system
• C: position of the camera center in the world coordinate system
• X−C: Translate, move the world origin to the camera center
• R: rotation matrix — aligns the world coordinate axes to the camera axes, This applies a rotation that aligns the world coordinate frame to the camera’s coordinate frame.
• t=−RC: camera position expressed as translation

---

So the transformation matrix becomes:

$$\left[\begin{array}{cc}\mathbf{R}& \mathbf{t}\end{array}\right]=\left[\begin{array}{cc}\mathbf{R}& -\mathbf{R}\tilde{\mathbf{C}}\end{array}\right]$$

---

• Why Apply Rotation After Translation?

 

• Translation affects origin (moves things)
• Rotation affects direction (reorients the frame)

We first move the origin to the camera (so the camera becomes the origin), and then rotate to align the camera's axes with the new origin.

---

$$\mathbf{R}\cdot \mathbf{X}+\mathbf{t}$$ can be rewritten using a matrix multiplication in this form:
$$\left[\begin{array}{cc}\mathbf{R}& \mathbf{t}\end{array}\right]\cdot {\mathbf{X}}_{\mathrm{hom}}$$
How?

1. We’re transforming a 3D point using:
$${\mathbf{X}}_{\mathrm{cam}}=\mathbf{R}\cdot \mathbf{X}+\mathbf{t}$$
R: 3×3 rotation matrix
𝑡: 3×1 translation vector
𝑋: 3×1 world coordinate

2. Let’s turn 𝑋 into homogeneous coordinates by appending a 1: $${\mathbf{X}}_{\mathrm{hom}}=\left[\begin{array}{c}X\\ Y\\ Z\\ 1\end{array}\right]\in {\mathbb{R}}^4$$
3. Augmented Matrix Form, We combine 𝑅 and 𝑡 into a single 3×4 matrix: $$\left[\begin{array}{cc}\mathbf{R}& \mathbf{t}\end{array}\right]=\left[\begin{array}{cccc}{r}_{11}& r_{12}& r_{13}& t_1\\ r_{21}& r_{22}& r_{23}& t_2\\ r_{31}& r_{32}& r_{33}& t_3\end{array}\right]$$
Then do the multiplication: $$\left[\begin{array}{cc}\mathbf{R}& \mathbf{t}\end{array}\right]\cdot \left[\begin{array}{c}X\\ Y\\ Z\\ 1\end{array}\right]=\mathbf{R}\cdot \left[\begin{array}{c}X\\ Y\\ Z\end{array}\right]+\mathbf{t}$$
4. Final equation : $$\mathbf{R}\cdot \mathbf{X}+\mathbf{t}⟺\left[\begin{array}{cc}\mathbf{R}& \mathbf{t}\end{array}\right]\cdot {\mathbf{X}}_{\mathrm{hom}}$$

---

• Camera Coordinates to Image (Intrinsics)

Now that the point is in the camera frame, we project it into the image using the intrinsic matrix 𝐾:$${\mathbf{x}}_{\mathrm{hom}}=\mathbf{K}\cdot \left[\begin{array}{cc}\mathbf{R}& \mathbf{t}\end{array}\right]\cdot \mathbf{X}$$

---

• Final Form: Projection Equation

$${\mathbf{x}}_{\mathrm{image}}=\mathbf{K}\cdot \mathbf{R}\cdot [\mathbf{I}\mid -\tilde{\mathbf{C}}]\cdot {\mathbf{X}}_{\mathrm{world}}$$

The reason why we use $[I\mid -\tilde{C}]$ instead of $[R\mid t]$

Because:

- It emphasizes that you're expressing everything relative to the camera center.
- It separates camera pose (center $\tilde{C}$) and rotation 𝑅.

---

BUT!!!! there is another formulation.

$$w\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=\left[\begin{array}{c}X\\ Y\\ Z\\ 1\end{array}\right]\cdot P,\mathrm{where}P=K\cdot [R\mid t]$$

 

Project world coordinates (X,Y,Z) to image pixel coordinates (x,y) via:

• Intrinsic matrix K: focal length, principal point
• Extrinsic matrix [R  ∣  t]: rotation + translation from world to camera

---

The difference between two of them above is

$${\mathbf{x}}_{\mathrm{image}}=\mathbf{K}\cdot \mathbf{R}\cdot [\mathbf{I}\mid -\tilde{\mathbf{C}}]\cdot {\mathbf{X}}_{\mathrm{world}}$$

is explicitly uses the camera center C in world coordinates. 

---

With Camera Center C	Standard Projection
P=K⋅R⋅[I ∣ −C]	P=K⋅[R ∣ t]

 

You want to...	Use...
Work with camera position explicitly	P=K⋅R⋅[I ∣ −C]
Use calibration output or toolbox	P=K⋅[R ∣ t]

 

https://intuitive-robotics.tistory.com/110

https://velog.io/@noogoolgga/Camera-model

https://darkpgmr.tistory.com/107